Vectorization - How to Vectorize ML Algorithms with MATLAB
Jun 16, 2020

In my previous post, I gave a simplified introduction to Machine Learning for beginners. It therefore brings the need for me to write a post on “Vectorization”. You might be hearing it for the first time or you have possibly come across it sometime. Either one of those, I can tell you that it isn’t a difficult subject, in fact in the field of Machine Learning I found it much easier than a normal iterative code (for & while loop). Now lets begin, by the end of this post I want you to understand what vectorization is, it’s application and how to use it in your ML Implementation.
The title of this post actually says “Vectorization in ML with MATLAB”, so you can tell I would be teaching you how to vectorize your code with MATLAB as the programming language, but you should know that almost all language codes can be vectorized. Now let’s look at a simplified definition of vectorization.
Vectorization is a method of writing codes that makes them run much faster. It applies operators to “multiple” operands without the use of loops, these operands are usually a matrices or vectors.
A more official definition, cited from Quantifisolutions website.
Vectorization is the process of converting an algorithm from operating on a single value at a time to operating on a set of values (vector) at once.. In a vectorized calculation, all elements of the vector (array) can be added in one calculation step.
Now let’s look into a basic explanation for it. You want to perform calculations on some numbers or in our case, Data, you have to write a piece of code to do the computation for you. In Machine Learning, 80% of the code we are writing is an iterative function, looping over a fixed number of training examples or sort. For example, in Linear Regression, to build a model or predictor we have to compute the cost function and gradient descent over all our training data, and to do this we more than likely need to use loops, that’s where vectorization comes in. Let’s look at what makes vectorization possible in Machine Learning. We would be touching mainly on Matrix and Vectors in this post.
Matrices are in simple form two-dimensional arrays. That is, they are made up of numbers in a 2D shape or size.Matrices are usually denoted by uppercase names in Matlab.
Arrays(Wikipedia) on the other hand is a set of numbers arranged in list format, as such, a Matrix can be called an array but not the other way round, simply because a Matrix although being in 2D shape is still a list of numbers in “rows” and “columns”. Let’s take an example so you can understand better.
Vectors are one-dimensional arrays. They are similar to matrix with the exception that they have only 1 dimension. So basically, a Vector is a matrix with one column and many rows. So vectors are a subset of matrices.
Scalars on the other hand means that an object is a single value, not a vector or matrix. In other words, real numbers or integer values like 2.
Example 1:
Array = [2,3,4,6,7,8] %list of num in square brackets
Matrix =[2,3,4;6,7,8] % 2x3 Matrix with 2 rows and 3 columns
Looking at the above example,
- You can write matrices by separating rows with semicolon(;)
- By adding a semicolon, we define a new row and also columns
- Not adding a semicolon makes it an array
Note: We have higher dimensions of Matrices in 3D, 4D etc,, you wouldn’t need to understand it for implementing Machine learning
Getting Familiar with Dimensions in Matrix
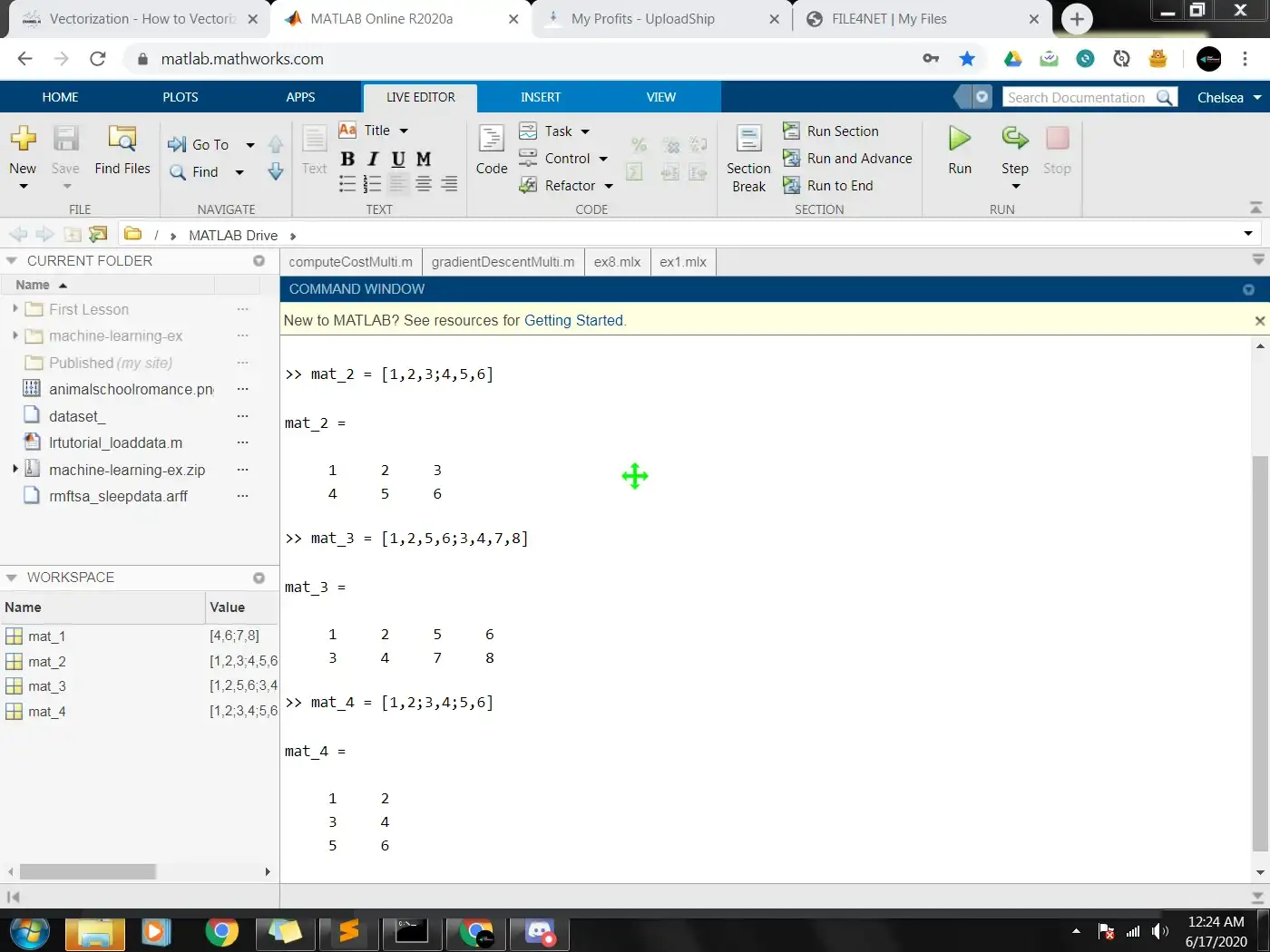
mat_1 = [4,6;7,8] % A 2x2 matrix (2 rows and 2 columns)
mat_2 = [1,2,3;4,5,6] % A 2x3 matrix (2 rows and 3 columns)
mat_3 = [1,2,5,6;3,4,7,8] % A 2x4 matrix (2 rows and 4 columns)
mat_4 = [1,2;3,4;5,6] % A 3x2 matrix (3 rows and 2 columns)
Check out the visualiztion of the Matrices above in the image below. This would give you a better sense of how they are formed or their structure.
Vectorization in Machine Learning is done or carried out when we want to perform calculations on Matrix-Matrix or Matrix-Vectors. Most of our data in ML is stored and read in rows and colums. In the code box below are some examples showing operations between matrix and Vectors, but before you learn about them I would like to list a few rules guiding how we carry out operations in matlab on matrices.
Rules Guiding how to Combine Arrays in Matlab
-
To add or subtract two matrices, their dimensions must be the same. You cannot use the Addition/Subtraction operator on Matrix of unequal dimensions. Example: Adding a 2x3 and 3x2 matrix throws an error. Addition on Matices are Element-wise, so you simply add or subtract each corresponding element.
-
Matrix-Vector Multiplication: The result is a vector. In a Matrix-Vector muliplication the number of “columns” of the matrix must be equal to the number of “rows” of the vector. An m x n matrix multiplied by an n x 1 vector results in an m x 1 vector.
-
Matrix-Matrix Multiplication: We multiply two matrices by breaking it into several vector multiplications and concatenating the result. An m x n matrix multiplied by an n x o matrix results in an m x o matrix. To multiply two matrices, the number of “columns” of the first matrix must equal the number of “rows” of the second matrix.
-
In scalar multiplication, we simply multiply every element by the scalar value, same applies for scalar addition or division.
Matrix-Vector Multiplication
% Initialize matrix A
A = [1, 2, 3; 4, 5, 6;7, 8, 9]
% Initialize vector v
v = [1; 1; 1]
% Multiply A * v
Av = A * v
Results:
A =
1 2 3
4 5 6
7 8 9
v =
1
1
1
Av =
6
15
24
Matrix-Matrix Multiplication
% Initialize a 3 by 2 matrix
A = [1, 2; 3, 4;5, 6]
% Initialize a 2 by 1 matrix
B = [1; 2]
% We expect a resulting matrix of (3 by 2)*(2 by 1) = (3 by 1)
mult_AB = A*B
Results:
A =
1 2
3 4
5 6
B =
1
2
mult_AB =
5
11
17
Example 2:
vect_1 = [1;2;3;6;7;8] % A column vector with 6 values
mat_1 = [1,3,5;8,7,6] % A 2x3 Matrix
REASONS FOR VECTORIZING CODE
- Appearance: Vectorized mathematical code appears more like the maths we are used to from high-school, making the code easier to understand.
- Less Error Prone: Without loops, vectorized code is often shorter. Fewer lines of code mean fewer opportunities to introduce programming errors.
- Performance: Vectorized code often runs much faster than the corresponding code conatining loops
Now that we have gone over a few reasons for using vectorized codes, I would like to show you code that outlines the difference in using loops vs vectorization for writing codes. This alone would show you the main idea of vectorization. Although you should know that as model size increases, so does the technique for carrying out vectorization. It gets more advanced but to tell the truth, it’s nothing you can’t handle, as long as you are doing Machine Learning, the concept remains the same as the example below. Let’s write code.
Example 4:
This code computes the sine of 1001 values ranging from 0 to 10:
Using Loops:
i = 0;
for t = 0:.01:10
i = i + 1;
y(i) = sin(t);
end
Using Vectorization:
t = 0:.01:10;
y = sin(t);
So there you have it, a few example codes and reasons, more than sufficient why it is advised to vectorize code when Implementing ML. Now that you’ve learnt the basics of Matrix, vectors and code vectorization you can now ahead and use this concept in your work. For reference, all the code for my last post in Linear regression were vectorized, so you can start learning from there how this works in ML and if you want a deeper understanding, check out this course by Vanderblit University on Coursera: Introduction to Programming with MATLAB. It covers almost all you need to use Matlab to advanced level. I suggest you enroll if you want to use Matlab as your main programming lang for Machine Learning. Thanks for reading along, I do hope you learnt a thing or two about Vectorization. Even if u feel like you didn’t get much, don’t worry about it, all you need is some practice and you should understand it fully in a short while. If you have any questions related or closely related to our topic, I would very much like to hear it, simply leave a comment below.